Le mot d'introduction
Pendant cet été, certains de nos membres de Toulouse Dataviz ont traversé le Globe, ont voyagé en Australie et au Japon pour nous rapporter des visualisations singulières : un panneau d’avertissement d’incendie en plein outback ou de sangaku, un panneau de bois avec des défis mathématiques. Ces visualisations lancent de nombreux défis aux intrépides aventuriers, imperturbables kamis et aux différents pèlerins. Toujours à la recherche de visualisations exotiques, nous avons aussi ramené des gaufres, des barres à puces et autres essaims d’abeille.
Mais le temps file, c’est déjà la rentrée, l’automne pointe son nez. Nous vous proposons un meetup de témoignages le 3/10.
Meetup du 3 Octobre
- Laurent Tournier CEO de la société Tactic3D qui propose des logiciels de visualisation graphique de sport (football, basketball, rugby et handisport)
- Loïc Donot nous présente son expérience en visualisation de données et cartographie à la Direction départementale des territoires (DDT31)
- L'équipe TDV nous présentera aussi quelques news sur l'outil observablehq et sur des projets de dataviz en cours.
Ces présentations seront le support d’échanges concrets entre les participants. Comment avez vous fait ?
S'inscrire ici
Un étrange indicateur dans l’outback australien !

Quelles différences feriez-vous entre un danger grand, un très grand, un sévère, un extrême ou un catastrophique ? Auriez-vous un comportement diffèrent face à chacune de ces cinq indications ? Quelle confiance attribueriez-vous à cet indicateur inscrit à un panneau en plein arrière pays australien ? D’autant plus, si cet indicateur est mis à jour quotidiennement à la main ?
Un de nos membres en vadrouille dans l’outback australien a pris ce fameux panneau en photo. Il montre un danger d’incendie placé en niveau très élevé en plein milieu d’herbes desséchées et jaunies par l’impitoyable soleil austral. Pourriez-vous imaginer la couleur de l’herbe si cet indicateur nous alertait un danger extrême voire catastrophique ?
Ce singulier indicateur nous dit aussi que le danger d’incendie est permanent puisque le plus bas niveau est faible à modéré.
Cet indicateur est-il vraiment nécessaire ? La simple vue du paysage n’incite pas à allumer un barbecue.
Les diagrammes en gaufre
Qu’est-ce qu’un diagramme en gaufre?
Si vous pensiez que le diagramme sectoriel (camembert) et sa variante en anneau (donut) étaient les seuls types de data visualisation liés à la nourriture, détrompez-vous !
Il y a aussi le diagramme en gaufre (waffle chart).
Il s’agit d’une représentation composée de petits carrés colorés suivant les valeurs visualisées, de manière similaire aux secteurs colorés d’un camembert.
Ces carrés, disposés dans un rectangle, ressemblent à une gaufre, d’où le nom de ce diagramme.

Les principaux avantages
- Clarté et simplicité : Avec leurs grilles régulières, les diagrammes en gaufre sont faciles à lire et à comprendre pour un public non expert. Chaque cellule représente une fraction fixe, ce qui rend les comparaisons de proportions évidentes.
- Adaptabilité : Ils peuvent représenter différentes catégories ou parties d'un tout en un seul graphique, tout en conservant une structure compacte.
- Esthétique attrayante : Le côté "grille" donne un aspect net et moderne, ce qui rend cette visualisation particulièrement utile dans des présentations ou des rapports où l'impact visuel compte.

Les limites
- Estimation de la proportion exacte difficile : Si les gaufres donnent un aperçu rapide des relations entre les proportions, par contre, elles ne permettent pas de lire des valeurs exactes rapidement : compter les petits carrés un par un est laborieux. De plus les petits écarts sont difficiles à percevoir. Une solution consiste à afficher les pourcentages précis sous le graphique comme ci-dessous :

- Pas adaptés à toutes les données : Pour des ensembles de données avec des catégories nombreuses, un graphique en gaufre devient surchargé et perd en lisibilité. Voir ci-dessous :


Comment en créer un ?
- Sur excel : Exemple
- Sur Python avec la librairie pywaffle : Exemple
- Sur R avec {ggwagffle} : Exemple
- Sur PowerBI : Exemple
Créer des barres à puce dans Excel
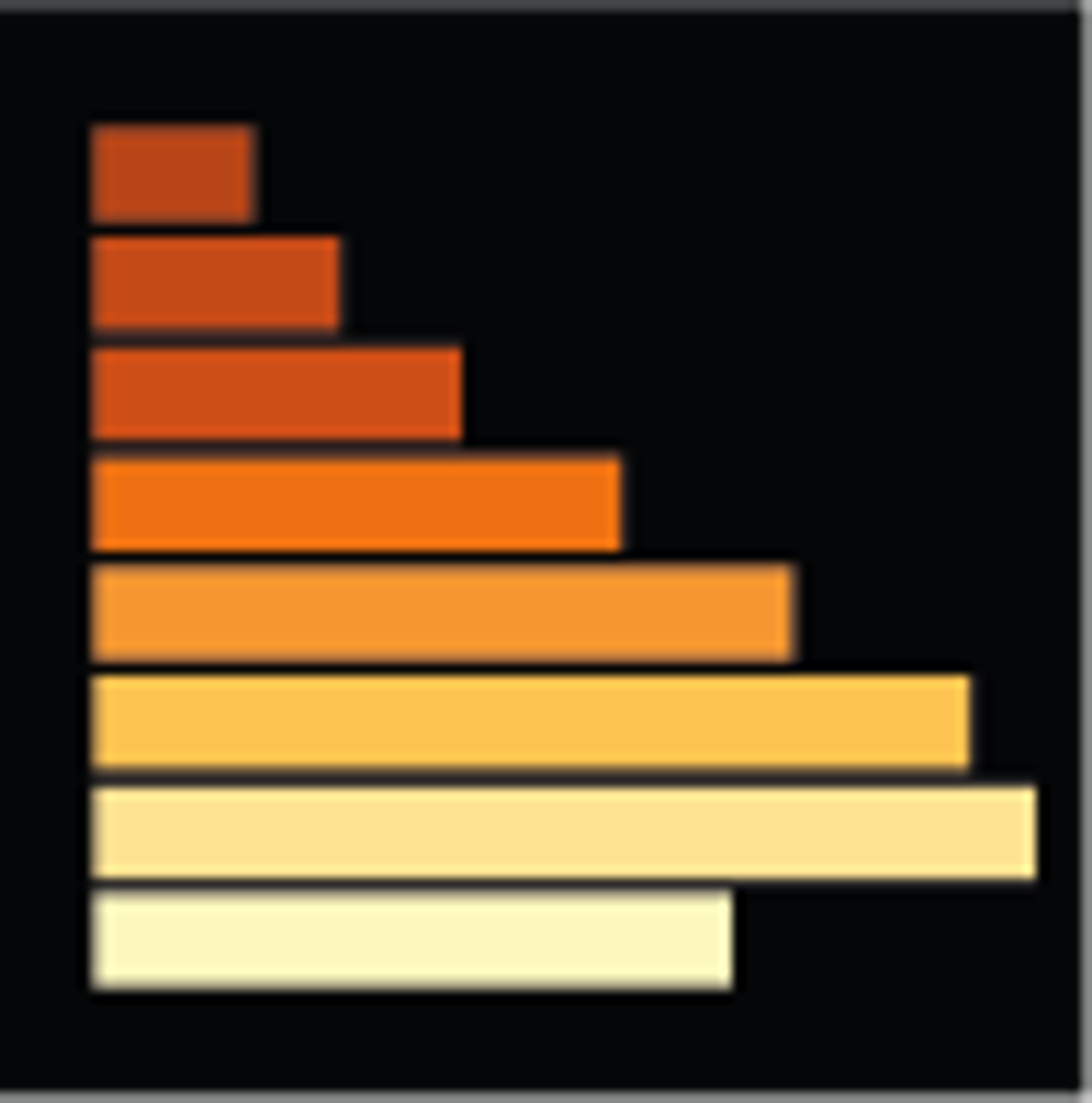
Vous devez réaliser la dataviz d’un tableau qui décrit l’écart entre le prévu et le réalisé (budget, avancement d’un projet, complétude d’une campagne de test, …). L’option proposée par défaut par Microsoft Excel, ce sont les horribles barres groupées.
Une alternative est le diagramme en barre à puce (bullet graph, bullet chart ou jauge). Proposé par Stephen Few dans The Bullet Graph design specification, ce diagramme figure les deux valeurs réalisées et espérées respectivement par une barre conteneur et une barre ou puce contenant.



Si l’excellent outil gratuit datawrapper permet de construire un tel diagramme en un clic de souris, cela est un peu plus compliqué sous Microsoft Excel. L’astuce est d’utiliser la capacité du tableur à tracer deux graphes l’un sur l’autre sur un axe principal et un axe secondaire. Pour les plus courageux, voici la procédure à suivre.
Soit une table de base en colonnes :
- Sélectionner la table, Insérer → barres 2D groupées horizontales
- Sélectionner la série ‘Réalisé’. Clic droit/ Format de la série de données. Dans le panneau de droite, choisir ‘axe secondaire’ → les barres se superposent
- Toujours dans la panneau de droite, ajuster la largeur de l’intervalle vers 200%
- Sélectionner la série ‘Budget’, ajuster la largeur de l’intervalle vers 40%, Remplissage ‘aucun’, Bordure ‘trait plein’
- Il est possible de fignoler en éliminant les échelles redondantes et pourquoi pas la légende devenue moins nécessaire puisque le contenant et le contenu deviennent objectivement visibles.
- Colorier les points qui dépassent en rouge. Les en retard en bleu. Double cliquer pour sélectionner que le point.
- Trier la table. Voilà
Ces manipulations sont à réaliser une fois.
Pour mettre à jour les données, il faut refaire la sélection avec un clic droit/ sélectionner des données. Si nécessaire, ajuster les largeurs d’intervalles.
Bonnes barres à puce dans votre tableur !
Climat et diagramme abeilles
.png?table=block&id=ba0f43e8-3962-4d17-a0fc-1f8b5fa38649&cache=v2)
C’est quoi un beeswarm?
Voila comment Philippe Rivière présente son beeswarm sur Observable :
”Dans un essaim d'abeilles, les points sont disposés le long d'un axe. Les points qui se superposent sont légèrement écartés de cet axe afin de conserver la lisibilité de la visualisation.
L'utilisation d'un moteur physique donne un aspect organique au graphique, au détriment d’une légère imprécision, les points se décalant également le long de l'axe horizontal et pas seulement dans la direction perpendiculaire”.

Exemple d’un diagramme en essaim d’abeilles
Voici un diagramme avec des multiples petits en essaim d’abeilles montrant la mesure de la température moyenne depuis 1940. Chaque point représente une mesure. La couleur correspond à la décennie de la mesure, du 1940 jusqu’à 2020.
Ces points sont disposés dans un diagramme en essaim où les points les plus à droite correspondent à des températures les plus élevées. Il y a 12 essaims pour chaque mois de l’année.
Le dégradé de couleur met en évidence l’augmentation des températures des dernières décennies. Les extrêmes qui se détachent appartiennent tous à la dernière décennie et même au deux dernières années. Un diagramme très visuel !
Comment réaliser un diagramme en essaim d’abeilles.
La plupart des outils de data visualisation intègrent la possibilité de créer ce type de diagrammes, comme par exemple :
- Tableau,
- RAWgraph,
- Excel ,
- Plot observable,
- R
- python.
Le billet du Japon
À l’occasion d’un court séjour à Nagano, ville connue pour ses Jeux Olympiques de 1998 et porte d’entrée des Alpes japonaises, je suis tombé sur ce panneau, exposé au musée du très beau sanctuaire de Zenkō-ji.

La partie supérieure du panneau est constituée de figures géométriques colorées. On y trouve des cercles tangents, des rectangles et des cercles combinés (comme dans la géométrie d’Euclide magnifiquement illustrée par Oliver Byrne), une iconographie très inattendue dans un temple…
Il s’agit là d’un rare panneau sangaku, un problème mathématique gravé sur un panneau de bois et exposé à l’entrée de certains sanctuaires shintô ou bouddhiste pendant la période Edo (entre 1600 et 1868). Leur fonction exacte n’est pas clairement établie, mais il s’agit bel et bien de problèmes mathématiques, le plus souvent géométriques, parfois très complexes. e sangaku présente une préface dans laquelle il est dit «Dans ce sanctuaire, nous demandons à dieu de nous aider à progresser dans nos connaissances mathématiques et lui dédions ce sangaku » (Princeton Weekly Bulletin, 2006).
Il pourrait s’agir d’offrandes aux kami ou au bouddha, de matière à réflexion pour les pèlerins ou encore d’une manifestation de la compétition intellectuelle entre mathématiciens, sectes ou écoles de pensée de l’époque. Ce mélange de respect et d’offrandes divines de problèmes mathématiques est unique à la religion shinto et illustre l’intrication de la religion dans la vie intellectuelle.
Certains de ces problèmes sont simples et se résolvent plus ou moins facilement mais d’autres ont résisté au temps et sont encore non démontrés ! Le texte sous le graphique explique le problème, donne la solution, mais ne donne jamais la preuve qui reste à déterminer par le lecteur.
Regardez cet exemple tiré d’histoires de mathématiques on le trouve au sanctuaire Isaniwa (Matsuyama) même s’il ne date que de 1937, il reflète bien l’esprit de ces sangakus
Étant donné un grand cercle et quatre cercles tangents à l’intérieur du grand, quel est le rayon du petit cercle rouge qui est tangent aux quatre cercles intérieurs ?

Un autre très bel exemple est reproduit ici sur un ema, petite plaquette votive que l’on peut acheter à l’entrée des temples pour écrire vœux, souhaits ou remerciements.

La formulation du problème (retranscrite ici est) :
Supposons que l’éventail de la figure soit 1/3 du cercle complet. Comme l’indique la figure : un cercle est, deux cercles ouest, deux cercles sud et deux cercles nord sont construits. Supposons le diamètre du cercle sud est donné. Quel est donc le diamètre du cercle nord (en rouge)? Les disques de même couleur ont le même rayon.
Formulé autrement, le problème est de calculer le rapport du rayon du cercle rouge au rayon du grand cercle délimitant l'éventail. La réponse est dans cet article.
Ces problèmes géométriques se trouvent également en Europe sous d’autres termes et dans de nombreux manuels et précis de géométrie. Le même problème se trouve d’ailleurs dans le livre des « récréations mathématiques » de Jacques Ozanam publié en 1694. Vous y trouverez d’ailleurs la solution (page 6).
On pourrait donc penser que les Japonais y ont puisé là leurs sources, cependant le Japon a été très isolé de l’occident et aucune de nos mathématiques n’y a pénétré à l’époque où furent écrites la plupart de ces songakus.
Toutes ces figures mathématiques exposées au grand public sont très belles et attirent forcément le regard et la curiosité du passant. Cela montre que la visualisation a toujours été un élément très important du développement des esprits, et des mathématiques, y compris au Japon.
━━━━━━━━━━━━━━━━━━
Cette newsletter de Toulouse-dataviz a été rédigée avec l'outil Notion que nous aimons bien. Si vous lisez cette newsletter et que vous n'êtes pas encore inscrit au club, il vous suffit de cliquer ici. Pour se désinscrire, demandez ici. Toutes les anciennes newsletters sont consultables ici. Vous pouvez aussi rejoindre nos communautés : Club ou Discord.
Merci à nos sponsors Clever Age, Vector, Pierre Fabre, Etincelle et perceptible qui soutiennent nos activités.